The Butterworth filter is an interesting filter in that its origin is based on the desire of a particular magnitude function. Butterworth (S. Butterworth, the Engineer in the 1930’s) demonstrated that the magnitude-squared function of
\[ \left| H\left( j \omega \right)\right|^2 = \dfrac{A^2}{1+\omega^{2n}} \]
has many admirable properties for use as a low-pass filter. To maintain consistency with Butterworth’s original paper and most academic treatments of the Butterworth filter, the filter is described as a prototype filter with unity gain and a cutoff frequency of \( \omega_c = 1 \) rad/s.
-The passband is the frequency spectrum of \( 0 \leq \omega \leq 1 \) rad/s
-The stopband is the frequency spectrum of \( \omega > 1 \)
-At the corner frequency \( \omega_c = 1\) rad/s, the magnitude response is always
\[|H(j\omega_c)| = \frac{1}{\sqrt{2}}=\;\; – 3 \text{ dB, for any filter order n.}\]
-Past the corner frequency \(\omega_c\) the magnitude response declines at a rate of \(-20 n \) dB/decade
-The magnitude response over frequency is monotonic (i.e. flat or decreasing) , thus no ripple.
Filter Realization
In order to realize a filter with the magnitude-squared response described above, we must solve for the transfer function H(s) and consequently the poles of H(s). The magnitude response of the Butterworth filter is the following
\[ \left| H\left( j \omega \right)\right|^2 = \dfrac{A}{1+\omega^{2n}} \]
\[ \left| H\left( j \omega \right)\right|^2 = H(j\omega)H(-j\omega) \]
Recalling that the frequency response is evaluated from \( s = j\omega \), the magnitude-squared of transfer function H(s) is of the form
\[ |H\left( s \right)|^2 = \dfrac{A}{1+(-1)^n s^{2n}} \]
The roots of the denominator of \( |H\left( s \right)|^2 \) contains the poles of H(s) as well as the poles of H(-s) which is a reflection of H(s) into the right-half-plane. The cumulative set of poles for both H(s) and H(-s) are the values of s which satisfy the relation
\[ 1 + (-1)^n s^{2n} = 0 \]
\[ s^{2n} = -(-1)^n \]
\[ s = ( -1(-1)^n)^{1/2n} \]
Butterworth showed that the general solution is a complex number of the general form
\[ s = e^{\left(j\pi k/2n\right)} \]
When n is even
\[ e^{\left(j\pi k/2n\right)} = (-1)^{1/2n} \]
\[ e^{j\pi k} = -1 \]
has the solution of
\[ k = 1, 3, 5, … \]
For the case where n is odd
\[ e^{\left(j\pi k/2n\right)} = (1)^{1/2n} \]
\[ e^{j\pi k} = 1 \]
has the solution of
\[ k = 0, 2, 4, … \]
From both the even and odd cases for n, one can observe that the general solution for the poles of H(s) lie on the unit circle (\(\omega_c = 1\)) dispersed equiangularly by an angle of \( \pi/n \) radians. Restricting the solution to the unique poles in left-hand-plane results in Butterworth’s general solution for the n poles \(p_k\), where k = 1,2,…,n as
\[ p_k = \sigma_k + j \omega_k \]
\[ \sigma_k = – \sin \left( \dfrac{2k-1}{2n} \pi\right) \]
\[ \omega_k = \cos \left( \dfrac{2k-1}{2n} \pi\right) \]
The figure below is a pole-zero map of H(s) for prototype filters of order 1 to 5. A pole is indicated as an “x” symbol. One will note all the poles lie on the unit circle (\(\omega_c = 1\)). All of the odd order filters (1,3,5) have a pole at -1 rad/s.
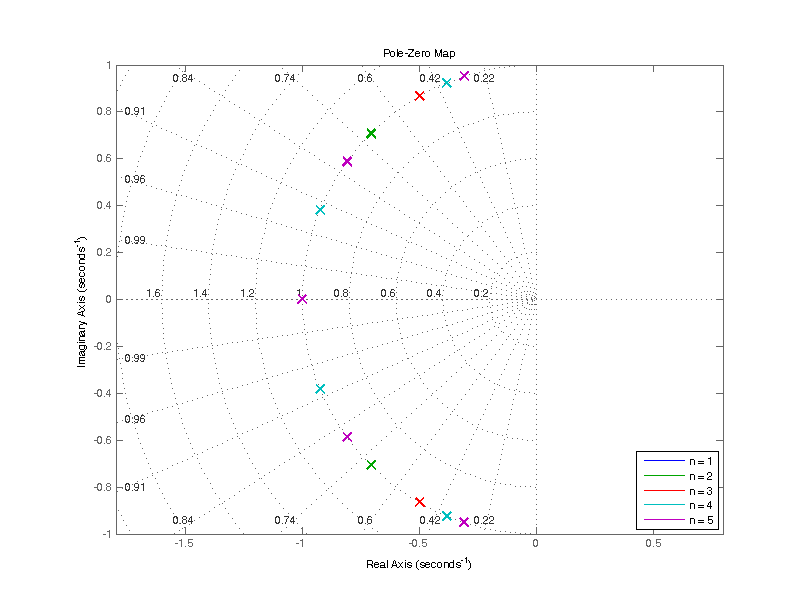
The location of the poles for prototype filters of orders 1 through 8 is shown in the table below.
| Filter Order n | Pole(s) | Pole(s) | Pole(s) | Pole(s) |
|---|---|---|---|---|
| 1 | -1 | |||
| 2 | -0.7071 ± 0.7071j | |||
| 3 | -1 | -0.5000 ± 0.8660j | ||
| 4 | -0.3827 ± 0.9239j | -0.9239 ± 0.3827j | ||
| 5 | -1 | -0.3090 ± 0.9511j | -0.8090 ± 0.5878j | |
| 6 | -0.2588 ± 0.9659j | -0.7071 ± 0.7071j | -0.9659 ± 0.2588j | |
| 7 | -1 | -0.2225 ± 0.9749j | -0.6235 ± 0.7818j | -0.9010 ± 0.4339j |
| 8 | -0.1951 ± 0.9808j | -0.5556 ± 0.8315j | -0.8315 ± 0.5556j | -0.9808 ± 0.1951j |
For the case that n is even, all the poles are complex pole pairs, the transfer function for n/2 complex pole pairs on the \( \omega_c \) circle in the left-hand-plane is as follows
\[ H(s) = \dfrac{1}{\left( s^2 + 2\delta_1 \omega_c s + \omega_c^2\right) \left( s^2 + 2\delta_2 \omega_c s+ \omega_c^2\right) …\left( s^2 + 2\delta_n \omega_c s + \omega_c^2\right) } \]
The damping factor of a complex pole pair is the following,
\[ \delta_k = \dfrac{- \mathbb{R}( p_k )}{\omega_c} \]
For the case that n is odd, an addition pole on the negative real axis at \(-\omega_c\) is added.
For example, the transfer function of a 7th order prototype filter with cutoff frequency \(\omega_c=1\), is the following
\[ H(s) = \dfrac{1}{\left(s+1\right)\left( s^2 + 0.445s +1 \right)\left( s^2 + 1.247s +1 \right)\left( s^2 + 1.802s +1 \right)} \]
An 8th order prototype filter with cutoff frequency \(\omega_c=1\), is the following
\[ H(s) = \dfrac{1}{\left(s^2 + 0.390s+1\right)\left( s^2 + 1.111s +1 \right)\left( s^2 + 1.663s +1 \right)\left( s^2 + 1.962s +1 \right)} \]
Magnitude Response
The butterworth filter does not have the sharpest transition from passband to stopband in contrast to some filters like a Chebyshev or an elliptic filter, but it is maximally flat in the passband. The magnitude and phase response of various prototype filters ranging from 1st order to 5th order is plotted below.
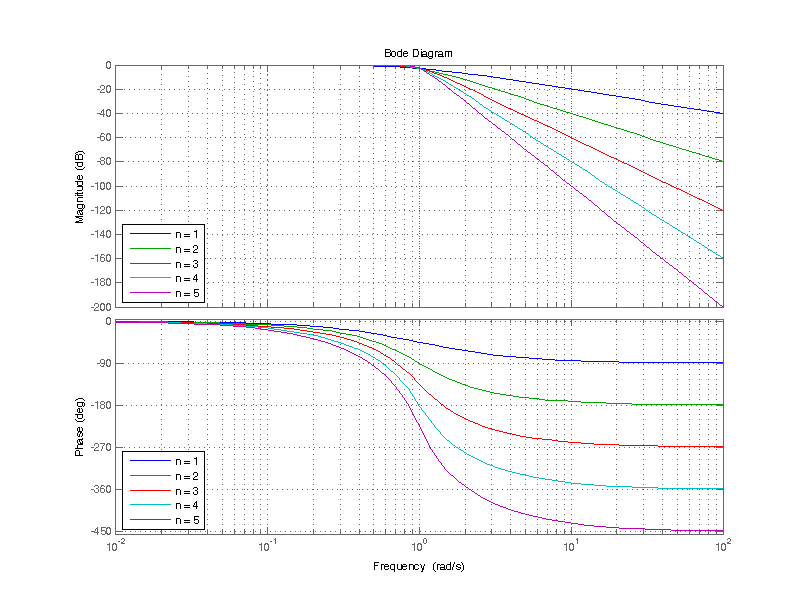
One of the most important attributes of a butterworth filter is difficult to observe on a log plot, that is that its flattness improves with filter order. A linear plot of the magnitude response near the corner frequency \( \omega_c =1 \) is shown below.
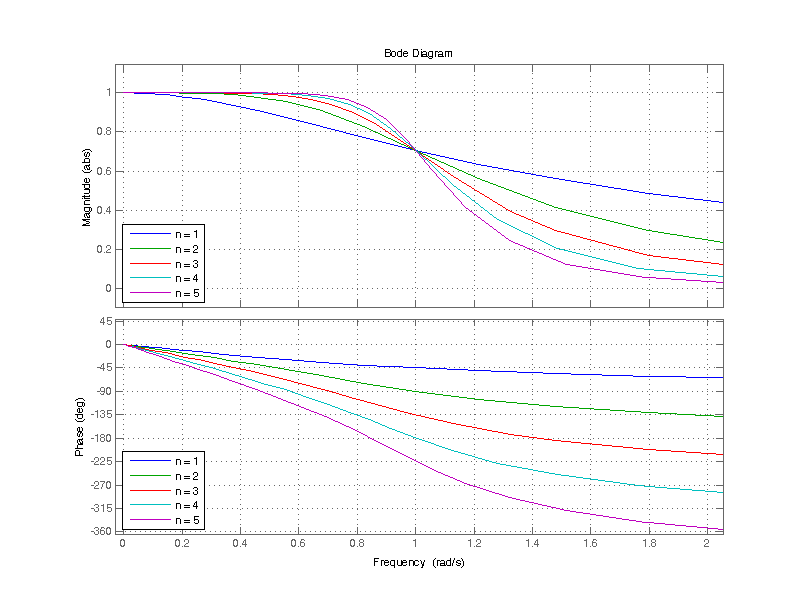
From this plot, at corner frequency \( \omega_c\) = 1 rad/s, the prototype filter \( H(j\omega) \) has a magnitude response of -3 dB (0.707) independent of the filter order n. Most importantly, the response becomes flatter as the filter order increases, in contrast to simply cascading n poles at \( \omega_c \), where the response “softens”.
The “sharpness” of the transition from pass-band to stop-band can be appreciated from the tabulated response below. At frequencies of 2 times the corner frequency, a 5th order filter provides 30 dB of attenuation. To contrast this figure, for a filter constructed as the cascade of 5 poles, doesn’t achieves 30 dB of attenuation until frequencies of 4.5 times that of the -3 dB point. Additionally, the cascaded pole filter only achieves 10 dB of attenuation at double the frequency of the -3 dB point.
| Normalized Frequency (w/p) | n=1 Magnitude (dB) | n=2 Magnitude (dB) | n=3 Magnitude (dB) | n=4 Magnitude (dB) | n=5 Magnitude (dB) |
|---|---|---|---|---|---|
| 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.5 | -1.0 | -0.3 | -0.1 | 0.0 | 0.0 |
| 0.9 | -2.6 | -2.2 | -1.9 | -1.6 | -1.3 |
| 1.0 | -3.0 | -3.0 | -3.0 | -3.0 | -3.0 |
| 1.1 | -3.4 | -3.9 | -4.4 | -5.0 | -5.6 |
| 1.5 | -5.1 | -7.8 | -10.9 | -14.3 | -17.7 |
| 2 | -7.0 | -12.3 | -18.1 | -24.1 | -30.1 |
| 5 | -14.1 | -28.0 | -41.9 | -55.9 | -69.9 |
| 10 | -20.0 | -40.0 | -60.0 | -80.0 | -100.0 |
Time-Domain Response
The phase non-linearity of the butterworth filter yields a non-uniform group-delay across the passband, which can be seen as ringing in response to a step input. Secondly, for filters of order 2 or greater the poles are complex pairs which are dampened oscillators in response to a step input.
The step-response to a unit input step for prototype filters of orders 1 through 5 is shown below.
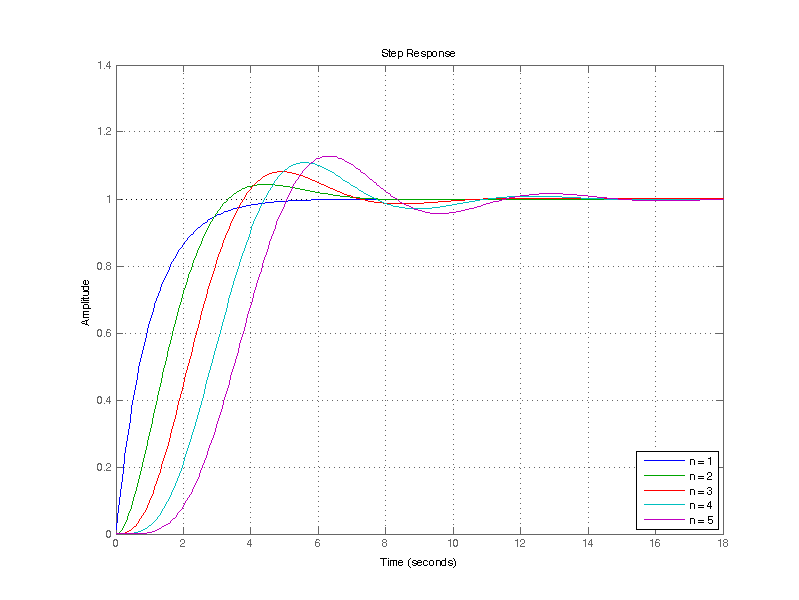
For the filter with 5th order, the least dampened complex pole-pair is (-0.3090 ± 0.9511j) with a corresponding Q of 1.62. The settling time is reflective of this pole’s Q, which requires approximately 1.6 cycles to decay to 0.2% of the peak oscillatory energy. In contrast, the highest Q pole of 20th order Butterworth filter, has a Q of 6.4.
| Filter Order | Rise Time [s] | Settling Time [s] | Overshoot [%] | Time to Peak [s] |
|---|---|---|---|---|
| 1 | 2.1973 | 3.9124 | 0 | - |
| 2 | 2.1490 | 5.9628 | 4.3 | 4.4513 |
| 3 | 2.2905 | 6.6376 | 8.1462 | 4.9311 |
| 4 | 2.4327 | 9.8727 | 10.8269 | 5.6213 |
| 5 | 2.5623 | 10.8386 | 12.7749 | 6.2950 |
Extra
Butterworth also showed that the coefficients can be calculated iteratively for the prototype case of \( \omega_c = 1\). The polynomial which satisfies the pole locations of a butterworth filter is as follows
\[ P(s) = a_0 + a_1 s + a_2 s^2 + … + a_n s^n \]
\[ a_0 = 1 \]
\[ a_k = \dfrac{\cos\left( (k-1)/2n\right)}{\sin\left( k \pi / 2n \right)} a_{k-1} \;\;\;\; k = 1,2,…,n\]
The transfer function of a prototype Butterworth filter is then simply
\[ H(s) = \dfrac{1}{P(s)} \]
Sample prototype filters of orders 1 through 6
\(1^{\text{st}}\) Order: \( H(s) = \dfrac{1}{ s + 1} \)
\(2^{\text{nd}}\) Order: \( H(s) = \dfrac{1}{s^2 + 1.414 s + 1} \)
\(3^{\text{rd}}\) Order: \(H(s) = \dfrac{1}{s^3 + 2 s^2 + 2 s + 1} \)
\(4^{\text{th}}\) Order: \( H(s) = \dfrac{1}{s^4 + 2.613 s^3 + 3.414 s^2 + 2.613 s + 1} \)
\(5^{\text{th}}\) Order: \( H(s) = \dfrac{1}{s^5 + 3.236 s^4 + 5.236 s^3 + 5.236 s^2 + 3.236 s + 1} \)
\(6^{\text{th}}\) Order: \( H(s) = \dfrac{1}{s^6 + 3.864 s^5 + 7.464 s^4 + 9.142 s^3 + 7.464 s^2 + 3.864 s + 1} \)