A tribute to the crustiest jellybean; and how powerful it still is.
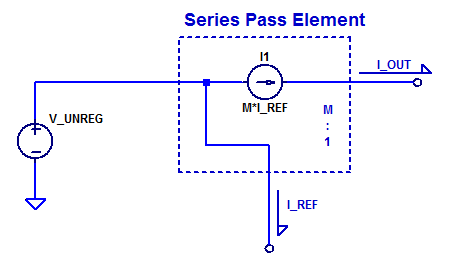
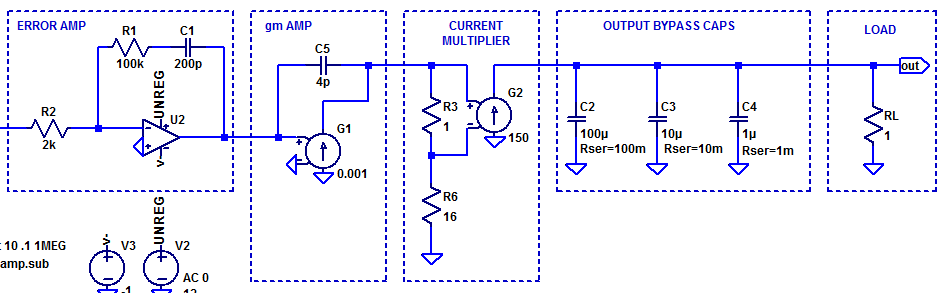
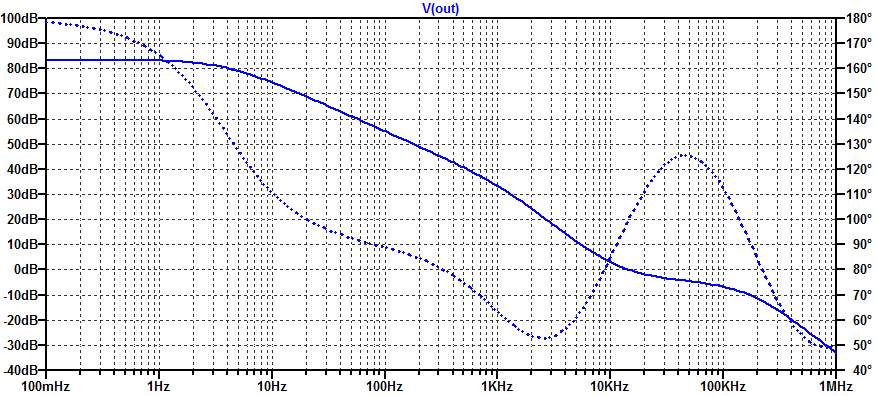
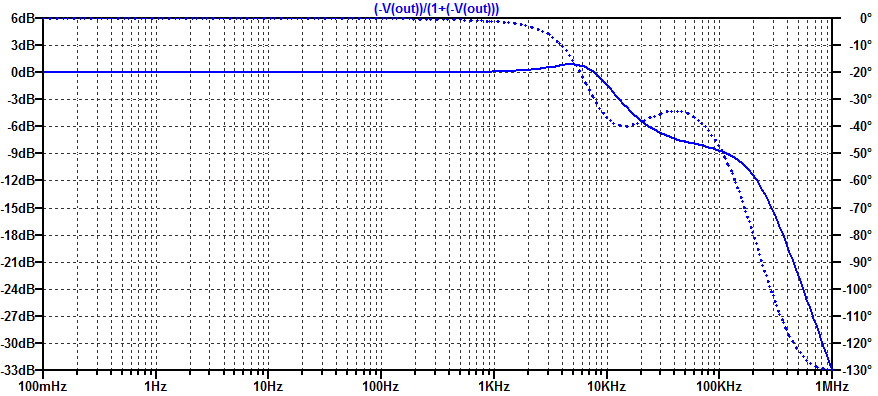
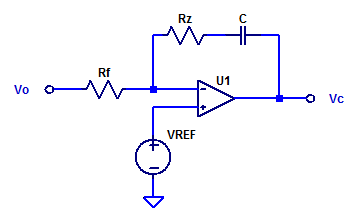
Continuing on from the analysis presented in low-noise-high-psrr-ldo-transconductance-gm-block, a simplistic trans-conductance amplifier can be constructed as shown in the figure below.
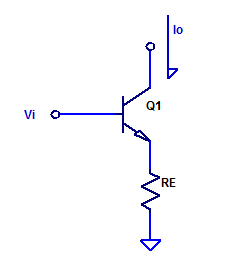
Forward trans-conductance from \( V_i \) to \( I_o \) was shown to be approximately,
$$ g_m = \dfrac{1}{R_E} \;\;\; \text{[A/V] } $$
For evaluation purposes, a \(g_m\) of 1 mA/V is chosen arbitrarily. The resistance of Re is then simply, Continue reading “Trans-conductance Amplifier Measurements”
The role of the series pass element is to supply a regulated current \( I_{out}\) from the unregulated input supply to the output load of the LDO. A simplified model of a current-mode series pass element is shown below.
Continue reading “Low-Noise, High-PSRR LDO – Series Pass Element”
A simplified model of the proposed LDO is shown in the figure below.
Loop gain of the simplified LDO model is shown in the figure below.
Note: not yet compensated more to come.
In this post we will develop and analyze a practical “type 2” error amplifier. The distinction of “type” 1, 2, or 3, is merely a description of how many poles are present in the compensator. All three types of error amplifiers will attempt to employ a pole at DC, i.e. operate as an integrator at low frequencies. Of course an error amplifier with an ideal integrator has a steady-state error of zero. However as is almost to all to common, digi-key does not stock any textbook class op-amps, with infinite differential gain and endless amounts of bandwidth.
The figure below illustrates a practical type 2 error amplifier with voltage input and voltage output.
Continue reading “Low-Noise, High-PSRR LDO – Error Amplifier”
Unfortunately there are no “ideal” capacitors in the Digi-Key catalog (maybe one day). As a result, we must select a diverse set of capacitors to attempt to construct a closer to ideal capacitor. Each capacitor can be represented by an lumped element RLC model. While one can go to many ends to construct the best capacitor model, for the purposes of this blog post, we limit our capacitor to only including an equivalent series resistance (ESR). Since we are only concerned with frequencies below 1 to 10 MHz, a series inductance of a few nanohenries is discarded.
A sample output load for a Low DropOut regulator (LDO) is shown in the figure below.
Continue reading “Low-Noise, High-PSRR LDO – Load Impedance”