Unfortunately there are no “ideal” capacitors in the Digi-Key catalog (maybe one day). As a result, we must select a diverse set of capacitors to attempt to construct a closer to ideal capacitor. Each capacitor can be represented by an lumped element RLC model. While one can go to many ends to construct the best capacitor model, for the purposes of this blog post, we limit our capacitor to only including an equivalent series resistance (ESR). Since we are only concerned with frequencies below 1 to 10 MHz, a series inductance of a few nanohenries is discarded.
A sample output load for a Low DropOut regulator (LDO) is shown in the figure below.
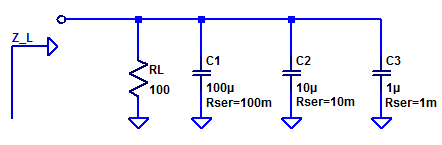
We see a nominal output load resistance \(R_L\) of 100 Ohms (chosen arbitrarily). Additionally a bank of parallel capacitors each one decade smaller than the previous. Note that the ESR also improves for each successively smaller capacitor. The impedance of each output element is then by inspection,
\[ Z_{RL} = RL \]
\[ Z_{C1} = R_{ESR1} + \dfrac{1}{sC_1} \]
\[ Z_{C2} = R_{ESR2} + \dfrac{1}{sC_2} \]
\[ Z_{C3} = R_{ESR3} + \dfrac{1}{sC_3} \]
The complete load impedance is then,
\[ Z_L = \left( \dfrac{1}{Z_{RL}} + \dfrac{1}{Z_{C1} }+ \dfrac{1}{Z_{C2} }+ \dfrac{1}{Z_{C3} }\right)^{-1} \]
The complete algebraic solution is left as an exercise to the reader (or your favorite spice simulator 🙂 )
Spice Simulation
Simulating the load impedance is accomplished by simply injecting an AC current test source. The complete LT-Spice schematic is shown below.
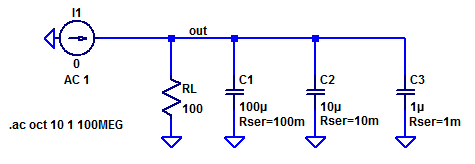
The load impedance is then simply \( V(out) / I(I1) \), the results are first plotted on a linear scale in the figure below.
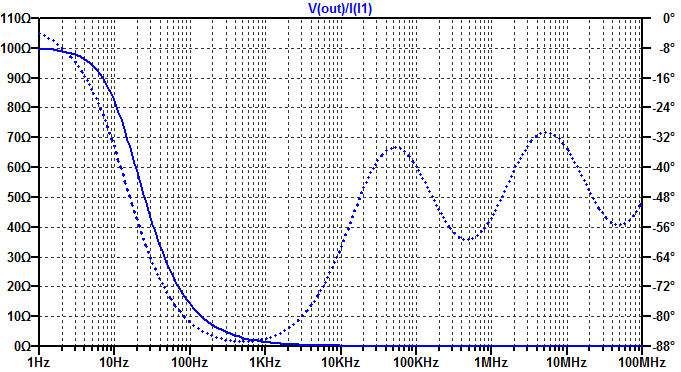
We see the low-frequency DC response is \(R_L\) as expected. Beyond that a linear scale does not provide much detail into the high-frequency behavior. The results plotted on a dB scale are shown below.
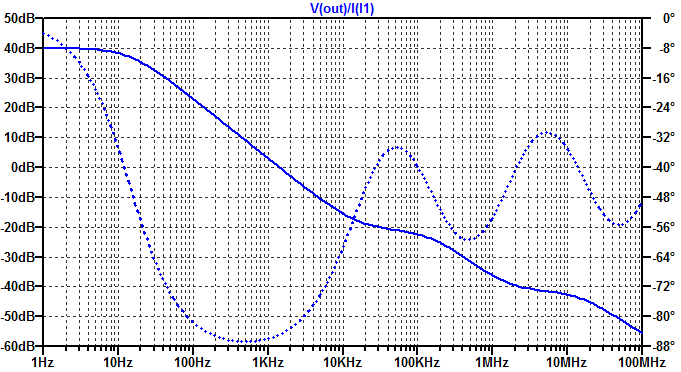
We see the impedance break from 100 Ohms to \( (j\omega C_1)^{-1} \) at approximately 10 Hz, and decline at 20 dB/decade. The impedance breaks again at approximately 10 kHz, where \( (j\omega C_1)^{-1} \) = \( R_{ESR1} \).
Transfer Function
For the purposes of a designing a custom discrete LDO, we wish to develop a transfer function of the LDO’s pass-element current to output potential (conveniently also impedance). We begin with a graphical interpretation of the load schematic introduced at the beginning of this post. The exact impedance is plotted in the figure below as \(Z_L(s)\). The impedance of each circuit element is also plotted as an overlay.
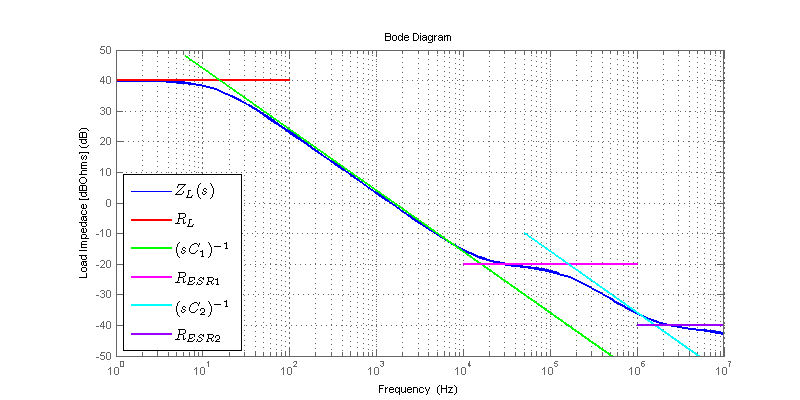
We note that provided \(R_L\) is >> \( R_{ESR1}\), the dominant pole is formed with \( R_L \; \& \; C_1 \), as
\[ p_1 = \dfrac{-1}{R_LC_1} \]
The first zero is formed with \( R_{ESR1} \) & \(C_1\), as
\[ z_1 = \dfrac{-1}{R_{ESR1}C_1} \]
The second pole is formed with \( R_{ESR1} \) & \(C_2\), as
\[ p_2 = \dfrac{-1}{R_{ESR1}C_2} \]
The second zero is formed with \( R_{ESR2} \) & \(C_2\), as
\[ z_2 = \dfrac{-1}{R_{ESR2}C_2} \].
It is perhaps worth emphasizing that the two zeros are in the left-hand plane and provide a phase boost (unlike those pesky right-hand plane zeros…)
The solution can be continued for any number of additional capacitors, however we are only concerned with poles/zeros within one to two decades above the unity gain crossover frequency for loop-gain. We target a design with maybe up to 100 kHz of loop bandwidth. Hence, we limit the results to the two poles and two zeros.
The approximate transfer function is then,
\[ V_o(s) = \dfrac{R_L\left(1+sR_{ESR1}C_1\right)\left(1+sR_{ESR2}C_2\right)}{\left(1+sR_{L}C_1\right)\left(1+sR_{ESR1}C_2\right)} I_o(s)\]
\[H(s) = Z_L(s) = \dfrac{R_L\left(1+sR_{ESR1}C_1\right)\left(1+sR_{ESR2}C_2\right)}{\left(1+sR_{L}C_1\right)\left(1+sR_{ESR1}C_2\right)}\]