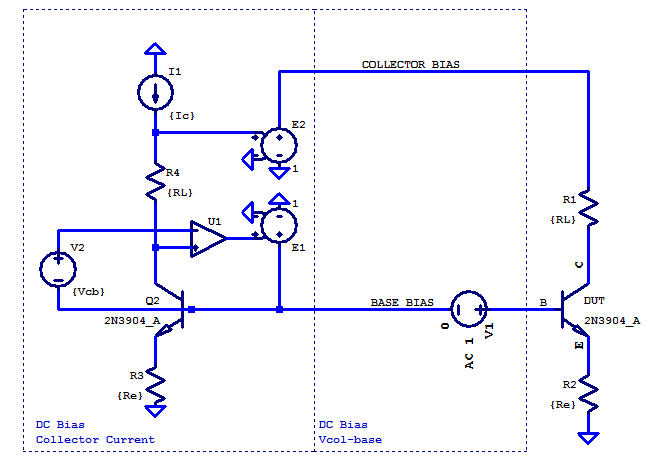
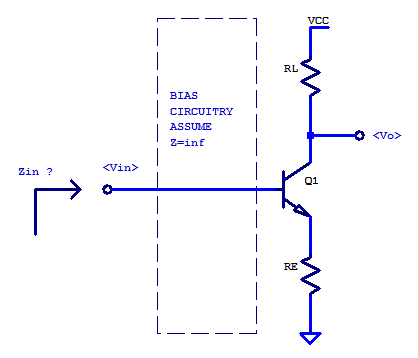
Note: Post Under-Construction, take as is…
Low-Frequency (non-reactive)
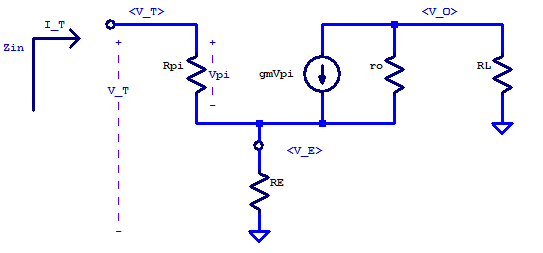
KCL at Ve
\[ I_T = \dfrac{V_E}{R_E} + \dfrac{V_E – V_o}{r_o} – g_m V_\pi \]
\[ V_\pi = r_\pi I_T \]
\[ I_T = V_E \left( \frac{1}{R_E} + \frac{1}{r_o} \right) – \dfrac{V_o}{r_o} – g_m r_\pi I_T \]
\[ \dfrac{V_o}{R_L} + g_m V_\pi I_T + \dfrac{V_o – V_E}{r_o} = 0 \]
\[ V_o \left( \frac{1}{R_L} + \frac{1}{r_o} \right) = \dfrac{V_E}{r_o} – g_m r_\pi I_T \]
\[ V_o = \dfrac{V_E}{r_o} \left( \dfrac{ R_L r_o}{R_L + r_o} \right) – g_m r_\pi I_T \left( \dfrac{ R_L r_o}{R_L + r_o} \right) \]
\[ I_T = V_E \left( \dfrac{R_E + r_o}{R_E r_o} \right) – \dfrac{V_E R_L}{r_o\left( R_L + r_o \right)} + \dfrac{g_m r_\pi R_L I_T}{R_L + r_o} – g_m r_\pi I_T \]
\[ V_E = \dfrac{ \left[ 1 + g_m r_\pi – \frac{g_m r_\pi R_L}{R_L + r_o}\right] }{\left[ \frac{R_E + r_o}{R_E r_o} – \frac{R_L}{r_o\left( R_L + r_o \right)} \right]} I_T \]
\[ V_T = V_\pi + V_E \]
\begin{align*}
R_{in} &= \dfrac{V_T}{I_T} \\
&= \frac{V_E}{I_T} + \frac{V_pi}{I_T} \\
&= \dfrac{ \left[ 1 + g_m r_\pi – \frac{g_m r_\pi R_L}{R_L + r_o}\right] }{\left[ \frac{R_E + r_o}{R_E r_o} – \frac{R_L}{r_o\left( R_L + r_o \right)} \right]} \frac{I_T}{I_T} + \dfrac{r_\pi I_T}{I_T} \\
&= \left[ \beta \left( 1 – \frac{R_L}{R_L + r_o} \right) \right] \dfrac{R_E r_o \left( R_L + r_o\right)}{\left( R_E + r_o\right)\left( R_L + r_o \right) – R_L R_E} + r_\pi
\end{align*}
When \( R_E << r_o \)
\[ R_{in} = \beta \left( 1 – \frac{R_L}{R_L + r_o} \right) R_E + r_\pi\]
\[ R_{in} \simeq \beta R_E + r_\pi\]
Circuit Equivalent Model
\[ R_i = \beta R_E \]
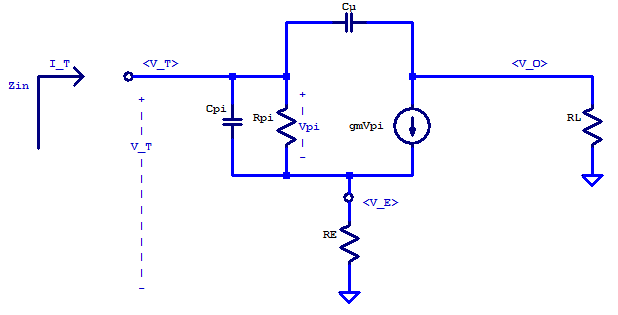
High-Frequency Model (grounded-emitter)
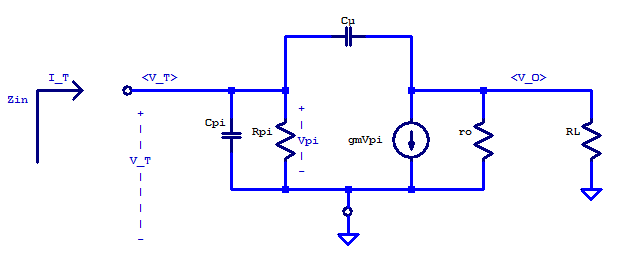
\[ I_T = \frac{V_T}{r_\pi} + s C_\pi V_T + \left( V_T – V_o \right) s C_\mu \]
\[ \dfrac{V_o}{R_L} + \dfrac{V_o}{r_o} + g_m V_T + \left( V_o – V_T \right)s C_\mu = 0 \]
\[ I_T = V_T \left( \frac{1}{r_\pi} + s C_\pi + s C_\mu \right) – V_o s C_\mu \]
\[ V_o \left( \frac{1}{R_L} + \frac{1}{r_o} + s C_\mu \right) = V_T \left( s C_\mu – g_m \right) \]
\[ V_o = V_T \dfrac{R_L r_o ( s C_\mu – g_m )}{R_L + r_o + R_L r_o C_\mu s } \]
\[ I_T = V_T \left( \frac{1}{r_\pi} + s C_\mu + s C_\pi \right) -V_T \dfrac{R_L r_o( s C_\mu ) ( s C_\mu – g_m )}{R_L + r_o + R_L r_o C_\mu s }\]
\[ V_T = \dfrac{ r_\pi( R_L + r_o + s R_L r_o C_\mu ) }{ R_L + r_o + s R_L r_o C_\mu – R_L r_o r_\pi(sC_\mu)(sC_\mu – g_m) + s r_\pi (C_\pi+C_\mu)(R_L + r_o + s R_L r_o C_\mu )} \]
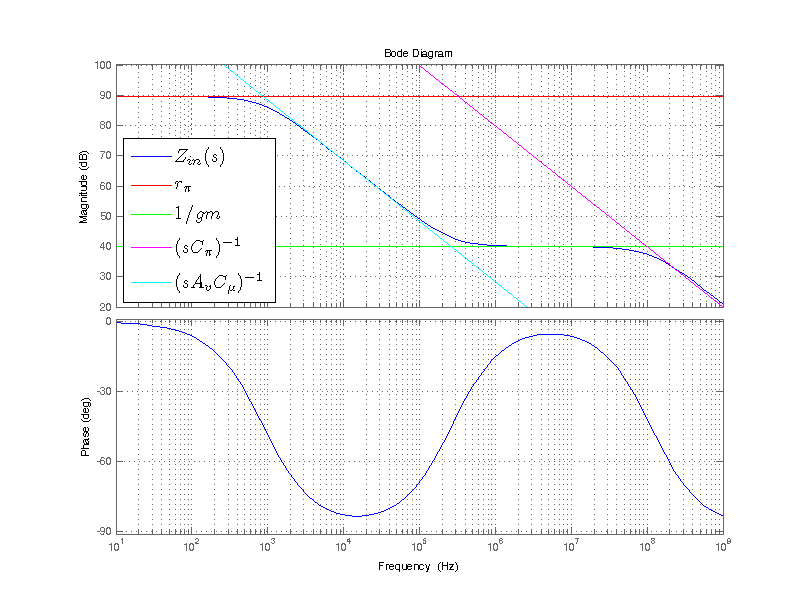
\[ Z_{in} = \dfrac{V_T}{I_T} \]
\[ Z_{in} = \dfrac{a_0 + a_1 s}{b_0 + b_1 s + b_2 s^2} \]
\begin{align*}
a_0 &= r_\pi ( R_L + r_o ) \\
a_1 &= r_\pi R_L r_o C_\mu \\
b_0 &= R_L + r_o \\
b_1 &= g_m r_\pi R_L r_o C_\mu + r_\pi( R_L + r_o ) C_\pi \simeq g_m r_\pi R_L r_o C_\mu \\
b_2 &= R_L r_o r_\pi ( C_\pi – C_\mu ) C_\mu
\end{align*}
\begin{align*}
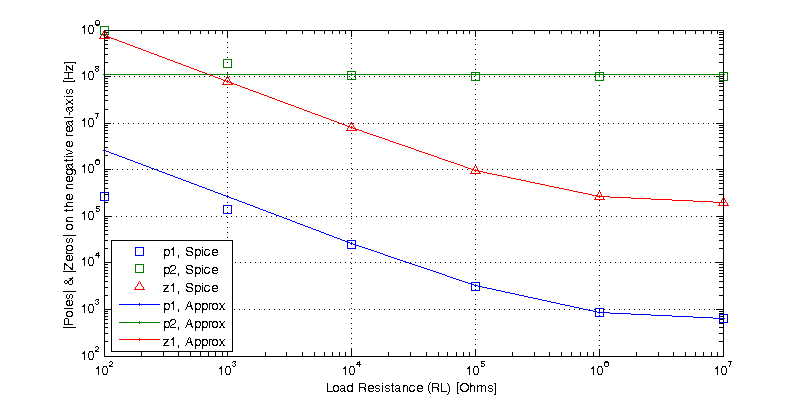
Z_1 &= \dfrac{-a_0}{a_1} \\
&= \dfrac{-r_\pi ( R_L + r_o ) }{r_\pi R_L r_o C_\mu} \\
Z_1 &= \dfrac{-1}{(R_L || r_o) C_\mu}
\end{align*}
\begin{align*}
P_1 &= \dfrac{-b_0}{b_1}\\
&= \dfrac{R_L + r_o}{g_m r_\pi R_L r_o C_\mu } \\
P_1&= \dfrac{-1}{ \beta ( R_L || r_o ) C_\mu }
\end{align*}
\begin{align*}
P_2 &= \dfrac{-b_0}{b_2 P_1}\\
&= \dfrac{(R_L + r_o)(-g_m r_\pi R_L r_o C_\mu)}{ R_L r_o r_\pi C_\mu ( C_\pi – C_\mu ) ( R_L + r_o) } \\
&= \dfrac{-g_m}{ C_\pi – C_\mu } \\
P_2 &\simeq \dfrac{-g_m}{ C_\pi }
\end{align*}
Circuit Equivalent Model
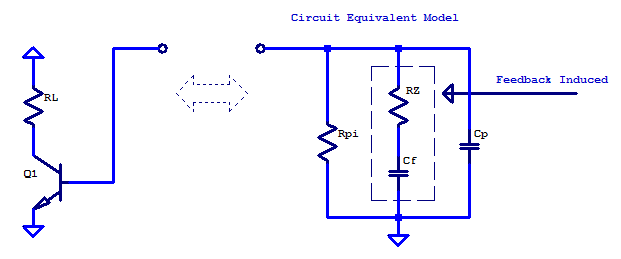
\[ P_a = \dfrac{-1}{r_\pi C_f} \;\;\; P_b = \dfrac{-1}{R_Z C_P } \;\;\; Z_a = \dfrac{-1}{R_Z C_f}\]
\begin{align*}
P_a &= P_1 \\
\dfrac{-1}{r_\pi C_f} &= \dfrac{-1}{ \beta ( R_L || r_o ) C_\mu } \\
C_f &= g_m (R_L|| r_o) C_\mu \\
C_f &= A_v C_\mu \;\;\; A_v = g_m (R_L|| r_o) \\
\end{align*}
\begin{align*}
Z_a &= Z_1 \\
\dfrac{-1}{R_Z C_f} &= \dfrac{-1}{(R_L || r_o) C_\mu} \\
R_Z &= \dfrac{(R_L || r_o) C_\mu}{g_m (R_L || r_o) C_\mu} \\
R_Z &= \dfrac{1}{g_m}
\end{align*}
\begin{align*}
P_b &= P_2 \\
\dfrac{-1}{R_Z C_P } &= \dfrac{-g_m}{ C_\pi } \\
C_P &= \dfrac{ C_\pi } {-\frac{g_m}{g_m}}\\
C_P &= C_\pi
\end{align*}
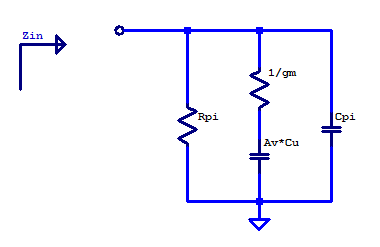
High-Frequency Model (Neglecting ro)
\[ \dfrac{V_o}{R_L} + g_m V_\pi + \left(V_o – V_T \right) s C_\mu = 0\]
Sub \( r_\pi || 1/(sC_\pi) \)
\[ \dfrac{V_E}{R_E} + \left( V_E – V_T \right)\dfrac{\left( 1 + s r_\pi C_\pi \right)}{r_\pi} = g_m V_\pi \]
\[ I_T = \left( \right)\dfrac{\left( 1 + s r_\pi C_\pi \right)}{r_\pi} + \left( \right) s C_\mu \]
\[ V_\pi = V_T – V_E \]
\[ V_o \left( \frac{1}{R_L} + s C_\mu \right) + V_T \left( g_m – s C_\mu \right) + V_E\left( -g_m \right) = 0 \]
\[ V_T \left(-\dfrac{\left( 1 + s r_\pi C_\pi \right)}{r_\pi} -g_m \right) + V_E \left( \dfrac{\left( 1 + s r_\pi C_\pi \right)}{r_\pi} + \frac{1}{R_E} + g_m \right) = 0\]
\[ V_o \left( -s C_\mu \right) + V_T \left(\dfrac{\left( 1 + s r_\pi C_\pi \right)}{r_\pi} +s C_\mu \right) + V_E \left( -\dfrac{\left( 1 + s r_\pi C_\pi \right)}{r_\pi} \right) = I_T\]
\[ Z_{in} = \dfrac{A_1 A_2}{b_0 + b_1 s + b_2 s^2 } \]
\begin{align*}
A_1 &= 1 + R_L C_\mu s \\
A_2 &= R_E + r_\pi + R_E g_m r_\pi + C_\pi R_E r_\pi s \\
b_0 &= 1 \\
b_1 &= R_E C_\mu + R_L C_\mu + r_\pi C_\pi + r_\pi C_\mu + R_E r_\pi g_m C_\mu + R_L r_\pi g_m C_\mu \\
b_2 &= R_L r_\pi C_\pi C_\mu + R_E r_\pi C_\pi C_\mu
\end{align*}
If the amplifier is has any modest voltage gain (eg. greater than 20 dB) then \( g_m R_L > 1 \), which allows for coefficient \( b_1 \) to be simplified.
\begin{align*}
g_m R_L &> 1 \\
R_L &> \frac{1}{g_m} \\
\beta R_L &> \frac{\beta}{g_m} \\
\beta R_L &> r_\pi \\
\end{align*}
\[ b_1 = \beta C_\mu ( R_E + R_L ) + r_\pi ( C_\pi + C_\mu ) \]
\[ b_1 \simeq \beta C_\mu( R_E + R_L ) \]
\begin{align*}
P_1 &= \dfrac{-b_0}{b_1} \\
&= \dfrac{-1}{\beta(R_E + R_L )C_\mu } \\
\end{align*}
\begin{align*}
P_2 &= \dfrac{-b_0}{b_1} \\
&= \dfrac{-\beta(R_E + R_L )C_\mu}{r_\pi C_\pi C_\mu ( R_E + R_L ) } \\
&= \dfrac{-g_m}{C_\pi}
\end{align*}
\begin{align*}
A_1(s)|_{Z_1 =s } &= 0 \\
Z_1 &= \dfrac{-1}{R_L C_\mu }
\end{align*}
\begin{align*}
A_2(s)|_{Z_2 =s } &= 0 \\
Z_2 &= \dfrac{-( R_E + r_\pi + \beta R_E) }{R_E r_\pi C_\pi }\\
Z_2 &= \dfrac{-(1/g_m + R_E )}{ (1/g_m)R_E C_\pi }\\
Z_2 &= \dfrac{-1}{ (R_E || 1/g_m) C_\pi }
\end{align*}
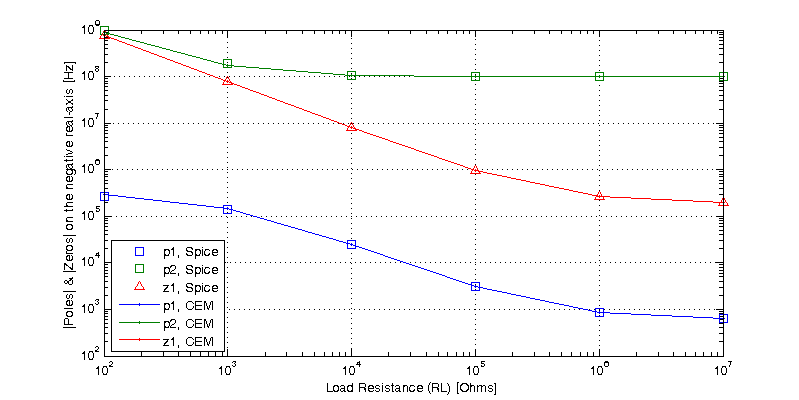
Circuit Equivalent Model
A model which provides two poles and two zeros is shown in the figure below.
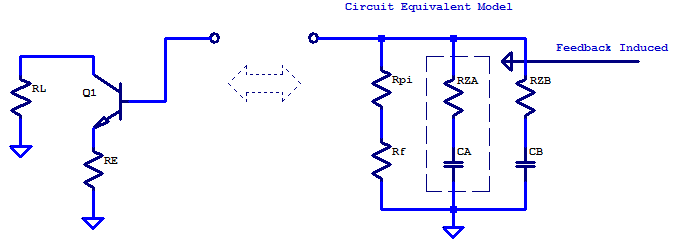
\[ z_a = \dfrac{-1}{R_{ZA} C_A } \]
\[ z_b = \dfrac{-1}{R_{ZB} C_B } \]
\[ p_a = \dfrac{-1}{ (r_\pi + R_f) C_A } \]
\[ p_b = \dfrac{-1}{ R_{ZA} C_B } \]
Beginning with the DC input resistance, \( R_f \) of the circuit equivalent model is
\begin{align*}
R_in &= r_\pi + R_f \\
R_in &= \beta R_E + r_\pi \\
R_f &= \beta R_E
\end{align*}
Equating dominate poles for CEM element \( C_A \)
\begin{align*}
p_a &= p_1 \\
\dfrac{-1}{(r_\pi + R_f)C_A} &= \dfrac{-1}{ \beta ( R_E + R_L ) C_\mu } \\
C_A &= \dfrac{\beta(R_E + R_L )C_\mu}{(r_\pi + \beta R_E)} \\
&= \dfrac{R_E + R_L }{1/g_m + R_E}C_\mu \\
\end{align*}
When \( R_L >> R_E \), \(C_A\) can be approximated as
\begin{align*}
C_A &= \dfrac{g_m}{1 + g_m R_E} R_L C_\mu \\ \\
g_{m,degen} &= \dfrac{g_m}{1 + g_m R_E} \\ \\
C_A &= g_{m,degen} R_L C_\mu
\end{align*}
Equating the first zero of \(Z_{in}\) to \(z_a\), CEM element \(R_{ZA}\) can be found to be
\begin{align*}
z_a &= z_1 \\
\dfrac{-1}{R_{Z1} C_A} &= \dfrac{-1}{R_L C_\mu } \\
R_{Z1} &= \dfrac{R_L C_\mu}{g_{m,degen} R_L C_\mu} \\
R_{Z1} &= \dfrac{1}{g_{m,degen}}
\end{align*}
Equating the second pole of \( Z_{in} \) to \(p_b\), the CEM element \(C_B\) can be solved as
\begin{align*}
p_b &= p_2 \\
\dfrac{-1}{R_{Z1} C_B} &= \dfrac{-g_m}{ C_\pi } \\
C_B &= \dfrac{C_\pi}{g_m R_{Z1}} \\
C_B &= \left( \dfrac{g_{m,degen} }{ g_m }\right) C_\pi \\
\end{align*}
Equating the second zero of \( Z_{in} \) to \(z_b\), the CEM element \(R_{Z2}\) can be solved as
\begin{align*}
z_b &= z_2 \\
\dfrac{-1}{R_{Z2} C_B} &= \dfrac{-1}{(R_E || 1/g_m) C_\pi } \\
R_{Z2} &= \dfrac{(R_E || 1/g_m) C_\pi}{\left( \frac{g_{m,degen}}{g_m} \right) C_\pi} \\
R_{Z2} &= \dfrac{R_E (1/g_m) }{R_E + 1/g_m} \dfrac{g_m}{g_{m,degen}}\\
R_{Z2} &= \dfrac{R_E }{R_E + 1/g_m} \dfrac{1 + g_m R_E}{g_{m}}\\
R_{Z2} &= R_E\\
\end{align*}
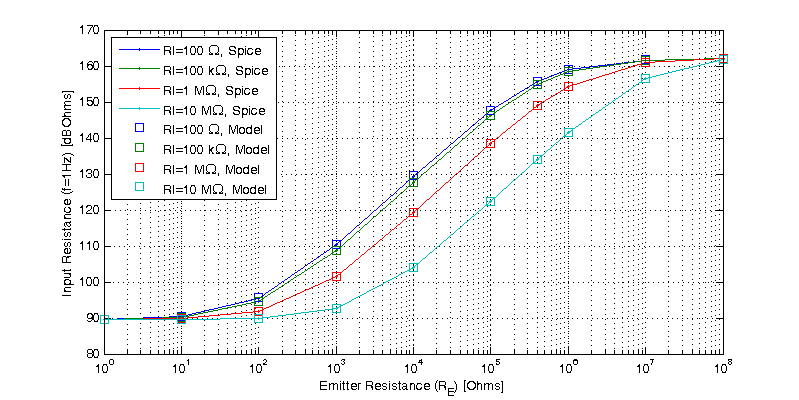
Spice Simulation