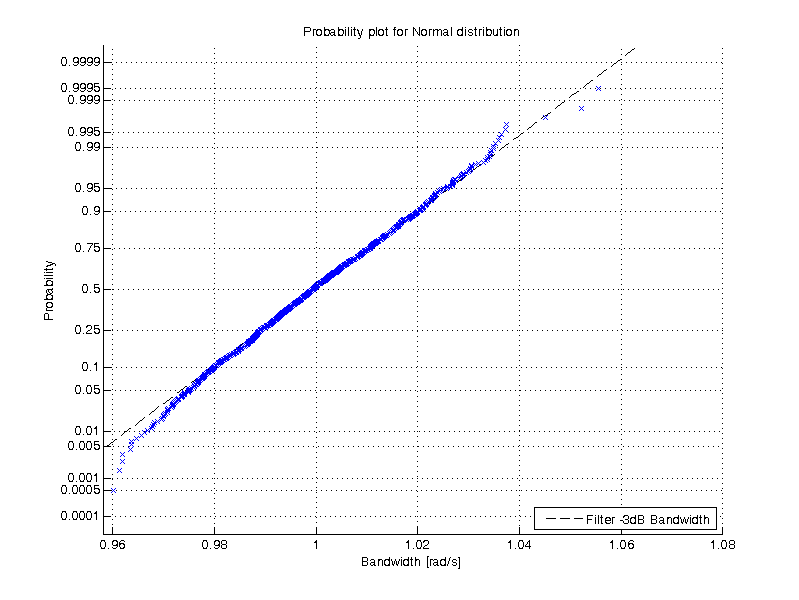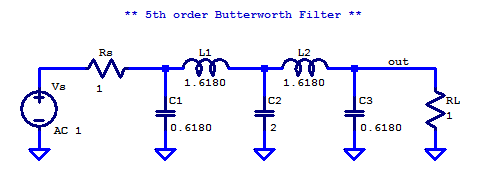
Monte-Carlo Simulation
Each of the discrete filter components is assumed to be normally distributed with \(\sigma = 0.02 \mu \).
\begin{align*}
R_S &\sim \mathcal{N}\left( 1, (0.02)^2 \right) \\
R_L &\sim \mathcal{N}\left( 1, (0.02)^2 \right) \\
L_1 &\sim \mathcal{N}\left( 1.6180, (1.6180 \cdot 0.02)^2 \right) \\
L_2 &\sim \mathcal{N}\left( 1.6180, (1.6180 \cdot 0.02)^2 \right) \\
C_1 &\sim \mathcal{N}\left( 0.6180, (0.6180 \cdot 0.02)^2 \right) \\
C_2 &\sim \mathcal{N}\left( 2, (2 \cdot 0.02)^2 \right) \\
C_3 &\sim \mathcal{N}\left( 0.6180, (0.6180 \cdot 0.02)^2 \right) \\
\end{align*}
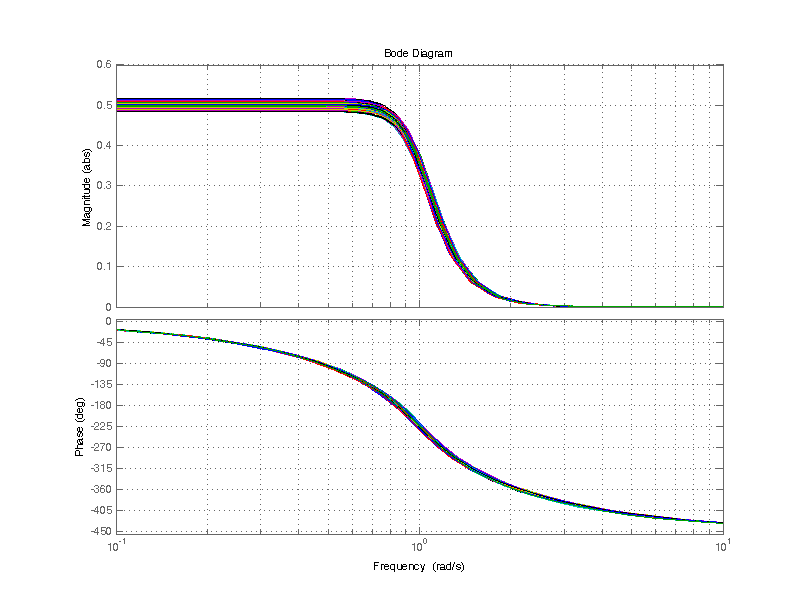
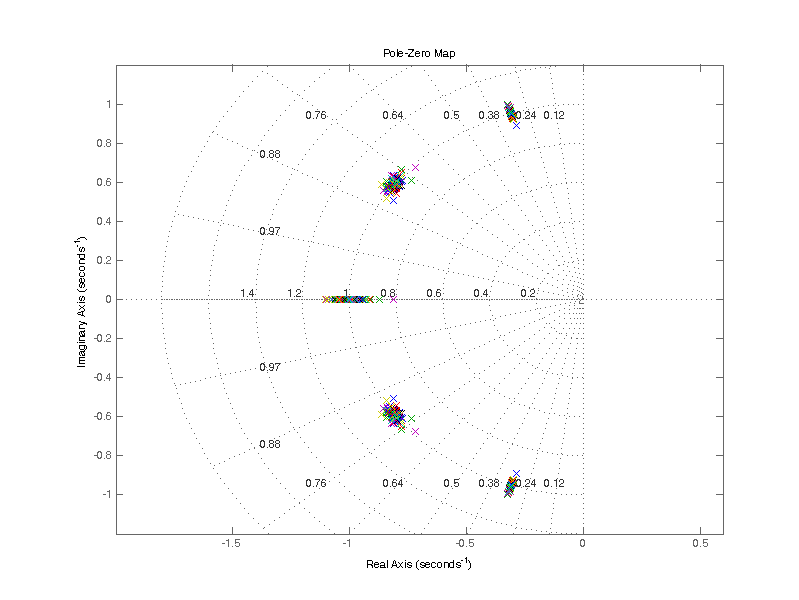
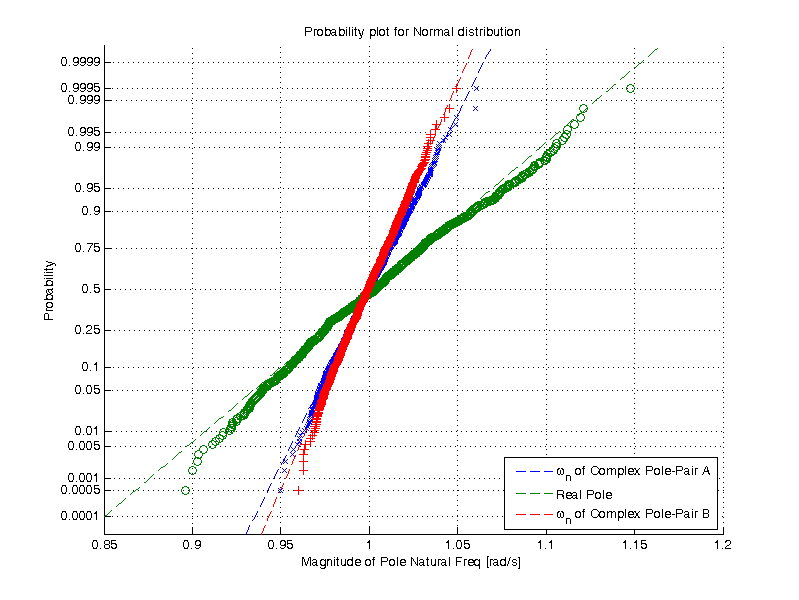
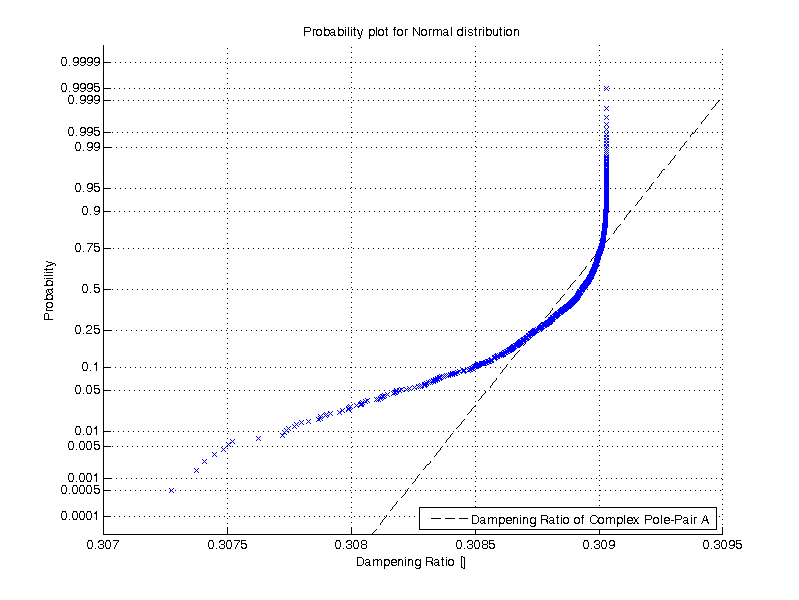
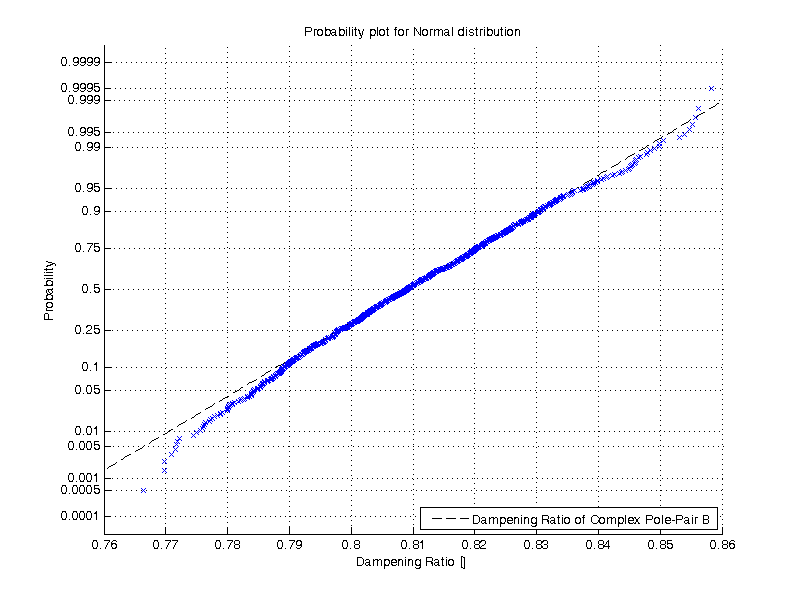
The bandwidth of the Butterworth filter: