A tribute to the crustiest jellybean; and how powerful it still is.
One of the simplest designs for a second order low-pass filter, is a RC ladder with 2 resistors and 2 capacitors. A drawback to this filters simplicity is that it requires a near ideal voltage source and a load with extremely high input impedance (ex. a buffer amplifier). A schematic of a second order RC low-pass filter is shown in the schematic below. Continue reading “RC Second Order Low-pass Filter”
For the general case of applying a filter between some signal source and load point, the solution space is constrained when the design is limited to only resistors and capacitors. For the sake of discussion, consider the schematic below. Here the signal source \(V_S\) has an output resistance of \(R_S\) and the filter is loaded by the input input resistance of the proceeding signal stage.
In some cases, the load resistance is negligible. For example the non-inverting input of an op-amp, when configured as a unity gain buffer has very high input resistance and only a small shunt capacitance. The output resistance of an 0p-amp, when operating closed-loop with negative feedback, is also a relatively low output resistance signal source. Other cases which have significant source resistance include a plethora of transducers, such as the electret condenser in a microphone. A load with significant input resistance is a loudspeaker, which provides a load resistance ranging from 4 ohms to 32 ohms.
In the general case, additional resistance in the signal path is often undesirable, as it limits the power transfer capability from source to load. Additional resistance whether it be in series or parallel to the load, yeilds additional signal attenuation from source to load, there by lowering the filtered signal level, which in turns degrades the Signal to Noise Ratio (SNR).
When the source resistance is significant, only an additional capacitor is required.
The Butterworth filter is an interesting filter in that its origin is based on the desire of a particular magnitude function. Butterworth (S. Butterworth, the Engineer in the 1930’s) demonstrated that the magnitude-squared function of
\[ \left| H\left( j \omega \right)\right|^2 = \dfrac{A^2}{1+\omega^{2n}} \]
has many admirable properties for use as a low-pass filter. To maintain consistency with Butterworth’s original paper and most academic treatments of the Butterworth filter, the filter is described as a prototype filter with unity gain and a cutoff frequency of \( \omega_c = 1 \) rad/s.
-The passband is the frequency spectrum of \( 0 \leq \omega \leq 1 \) rad/s
-The stopband is the frequency spectrum of \( \omega > 1 \)
-At the corner frequency \( \omega_c = 1\) rad/s, the magnitude response is always
\[|H(j\omega_c)| = \frac{1}{\sqrt{2}}=\;\; – 3 \text{ dB, for any filter order n.}\]
-Past the corner frequency \(\omega_c\) the magnitude response declines at a rate of \(-20 n \) dB/decade
-The magnitude response over frequency is monotonic (i.e. flat or decreasing) , thus no ripple.
One approach to improving stopband rejection is to cascade several first-order filters, there by achieving the combined rejection of n filters for better stopband rejection. While the implantation of such an arrangement is straight forward, there are some consequences to this approach which will be discussed below.
For a low-pass filter of the form
\[ H(s) = \dfrac{1}{1 + s/p} \]
From control theory the cascaded transfer function is just the multiplication of each filter transform. When each filter has an identical transfer function the overall transfer function is the following
\[ C(s) = \dfrac{1}{(1 + s/p)^n} \]
A single pole transfer function has the general from of
\[ H(s) = \dfrac{1}{1 + \frac{s}{p}} \]
Since H(s) has no roots in the numerator, the transfer function H(s) has no zeros. H(s) does have one root in the denominator, at
\[ s = -p \]
H(s) is said to have one pole at -p in the left-hand plane. As will be seen in the following sections, there are some important attributes for the magnitude and phase of a transfer function which can be generalized around the pole location.
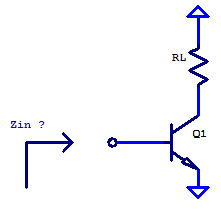
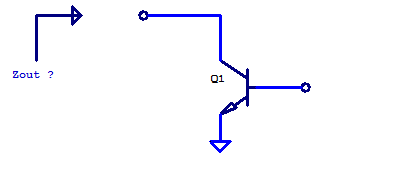In this post, a circuit equivalent model of the output impedance of a common-emitter amplifier will be developed. To begin, a low-frequency non-reactive model of the output resistance of a common-emitter (CE) amplifier will be solved. Proceeding models will include the capacitive elements of a CE amplifier. Separating the High-Frequency (HF) model into two distinct cases will allow for circuit analysis that is reasonable to perform by hand. The first HF model will be for when the base is ac-grounded and the emitter see a degeneration resistor. A second HF model is developed with a grounded emitter and with source resistance to the input (base) terminal. Concluding the post with a spice simulation to compare/validate the circuit equivalent models developed. The desired outcome of this post is to gain an intuition into what “it looks like” electrically speaking into the output of a CE amplifier.
Outline:
– Review of output resistance/impedance
– Low frequency model
– High Frequency Model – Grounded Base
– High Frequency Model – Grounded Emitter
– Spice Simulation
More to come.
10R,49R9,90R9,110R,121R,732R,909R,1k,2k21,4k99,9k09,10k,12k1,100k,110k
